Trippy Trefoils
Loday found a realisation of all the Stasheff polytopes, including the K4 one shown here. The vertices in 4 dimensions are permutations on 4 letters, so the polytope lies in the 3 dimensional plane x + y + z + w = 10 and the vertices are on the integer lattice.
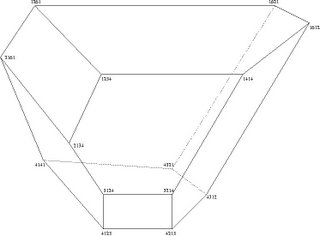 Loday also noticed that by tracing a curve around the faces, once through the pentagons and twice through the squares, one obtains a trefoil knot by judiciously choosing the crossings at the centre of the squares.
Loday also noticed that by tracing a curve around the faces, once through the pentagons and twice through the squares, one obtains a trefoil knot by judiciously choosing the crossings at the centre of the squares.
The classical Alexander knot invariant for the trefoil is obtained as follows. Let (t,-t,1,-1) be labels for the 4 region types: such as before undercrossing on left etc. Make a 3x5 matrix for the 3 crossings and the 5 regions of the trefoil knot, such as
-t t -1 0 1
-1 t 0 -t 1
0 1 -1 -t t
Now ignore 2 columns, take the determinant, and scale by powers of t appropriately, to obtain A(trefoil) = (t^-1) - 1 + t. The Jones polynomial can distinguish handedness for the trefoil knot. The left Jones polynomial is J(trefoil) = t + t^3 - t^4. Recall that the trefoil knot appeared recently in a heuristic discussion of the Koide formula for mass ratios. Here one uses the variable t=exp(a), which is the usual change of variables for Vassiliev invariants.
 Loday also noticed that by tracing a curve around the faces, once through the pentagons and twice through the squares, one obtains a trefoil knot by judiciously choosing the crossings at the centre of the squares.
Loday also noticed that by tracing a curve around the faces, once through the pentagons and twice through the squares, one obtains a trefoil knot by judiciously choosing the crossings at the centre of the squares.The classical Alexander knot invariant for the trefoil is obtained as follows. Let (t,-t,1,-1) be labels for the 4 region types: such as before undercrossing on left etc. Make a 3x5 matrix for the 3 crossings and the 5 regions of the trefoil knot, such as
-t t -1 0 1
-1 t 0 -t 1
0 1 -1 -t t
Now ignore 2 columns, take the determinant, and scale by powers of t appropriately, to obtain A(trefoil) = (t^-1) - 1 + t. The Jones polynomial can distinguish handedness for the trefoil knot. The left Jones polynomial is J(trefoil) = t + t^3 - t^4. Recall that the trefoil knot appeared recently in a heuristic discussion of the Koide formula for mass ratios. Here one uses the variable t=exp(a), which is the usual change of variables for Vassiliev invariants.






2 Comments:
09 10 06
Those damnable trefoils!
Hi kea, If Geometry is your thing
you'll enjoy
dialogues with Eide
(Geometry & Physics)
His posts are simply great, he'll welcome your comments, he'll keep an eye on your posts, and he'll be happy to take you to the next level
Post a Comment
<< Home