M Theory Lesson 298
A product of two Markov type limits 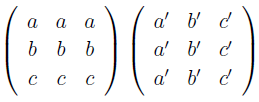 is one way of writing down a six parameter $3 \times 3$ matrix with distinct elements. For this matrix to be Hermitian, we require that $a' = \overline{a}$, $b' = \overline{b}$ and $c' = \overline{c}$, obtaining a six real parameter class of Hermitian matrices of the form $H = A A^{\dagger}$.
is one way of writing down a six parameter $3 \times 3$ matrix with distinct elements. For this matrix to be Hermitian, we require that $a' = \overline{a}$, $b' = \overline{b}$ and $c' = \overline{c}$, obtaining a six real parameter class of Hermitian matrices of the form $H = A A^{\dagger}$.
Note that a general complex transition matrix $M$, with fixed column sum, satisfies a Markov type rule: a column sum $S$ for $M$ goes to a sum $S^{2}$ for $M^{2}$. Thus for $S = 1$, the limiting operator still has the Markov property. For any such complex $M$, there is then associated a unique Hermitian matrix $A A^{\dagger}$, where $A$ is the long time limit. This process reduces the $6$ complex parameters of $M$ to $3$.
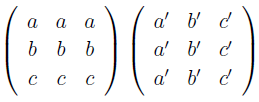 is one way of writing down a six parameter $3 \times 3$ matrix with distinct elements. For this matrix to be Hermitian, we require that $a' = \overline{a}$, $b' = \overline{b}$ and $c' = \overline{c}$, obtaining a six real parameter class of Hermitian matrices of the form $H = A A^{\dagger}$.
is one way of writing down a six parameter $3 \times 3$ matrix with distinct elements. For this matrix to be Hermitian, we require that $a' = \overline{a}$, $b' = \overline{b}$ and $c' = \overline{c}$, obtaining a six real parameter class of Hermitian matrices of the form $H = A A^{\dagger}$. Note that a general complex transition matrix $M$, with fixed column sum, satisfies a Markov type rule: a column sum $S$ for $M$ goes to a sum $S^{2}$ for $M^{2}$. Thus for $S = 1$, the limiting operator still has the Markov property. For any such complex $M$, there is then associated a unique Hermitian matrix $A A^{\dagger}$, where $A$ is the long time limit. This process reduces the $6$ complex parameters of $M$ to $3$.







0 Comments:
Post a Comment
<< Home