M Theory Lesson 71
I'm really not sure how useful this is, but since Moonshine Math is into the hexagon craze I thought I'd draw a decent picture of the annular Stasheff tiling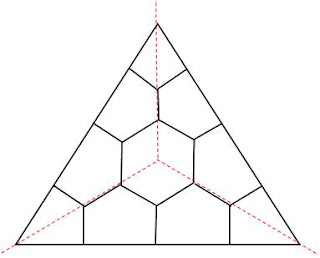 
with 6 edges on the interior and 12 on the outside. Recall that the red lines mark individual 3x3 matrix corners. By staring at this picture we see a 3D chair corner with a little cube cut out of it. Using very regular such triangles to tile a plane, and then forgetting the triangular boundaries, we obtain a regular hexagonal tiling with hexagons the size of the interior hexagons, because each triangle vertex gives one sixth of a hexagon. There is then a second hexagonal tiling with hexagons made out of 6 big triangles. The big hexagons are 27 times the area of the little ones, since there are $4 \frac{1}{2}$ hexagons to a triangle.
Note that a perfectly regular honeycomb has a representative eigenvalue set of $(1,0,-1), (2,1,0)$ and $(0,-1,-2)$. This corresponds to the top vertex labelling $[ \frac{1}{2}, 1, - \frac{3}{2} ]$ which obeys the zero sum rule.
with 6 edges on the interior and 12 on the outside. Recall that the red lines mark individual 3x3 matrix corners. By staring at this picture we see a 3D chair corner with a little cube cut out of it. Using very regular such triangles to tile a plane, and then forgetting the triangular boundaries, we obtain a regular hexagonal tiling with hexagons the size of the interior hexagons, because each triangle vertex gives one sixth of a hexagon. There is then a second hexagonal tiling with hexagons made out of 6 big triangles. The big hexagons are 27 times the area of the little ones, since there are $4 \frac{1}{2}$ hexagons to a triangle.Note that a perfectly regular honeycomb has a representative eigenvalue set of $(1,0,-1), (2,1,0)$ and $(0,-1,-2)$. This corresponds to the top vertex labelling $[ \frac{1}{2}, 1, - \frac{3}{2} ]$ which obeys the zero sum rule.
posted by Kea | 12:49 PM
1 Comments:
Compare your Stasheff tiling triangle to some figures at
Klein's Quartic Curve, John Baez, July 28, 2006
http://math.ucr.edu/home/baez/klein.html
Your triangle could include a circle within the triangle like the figure between:
a - “By the way, this 168-element group is also known as PSL(3,Z/2) - the symmetries of the "Fano plane". This is another name for the projective plane over Z/2. It has 7 points and 7 lines, with 3 points on each line and 3 lines through each point. If you draw one of the lines as a circle, it looks like this picture from the Wikipedia article on finite geometries:
and
b - “A symmetry of the Fano plane is any function from points to points that sends lines to lines. Such symmetries can send any point to any other point, and even while not moving one point they can permute the 4 lines not containing that point in an arbitrary way, for a total of “
Your central hexagon can be divided into 12 triangles as the heptagon is into 14 triangles in the figure between:
a - “First, there's the obvious 7-fold symmetry of Klein's original picture, which matches the 7-fold symmetry of Burkard Polster's picture of the Fano plane“
and
b - “There are some subtleties. For example, rotating the central blue heptagon also has the effect of rotating each of the two blue heptagons near the edges. If you rotate the central heptagon 1/7 of a turn, one of the other heptagons rotates 2/7 of a turn and the other rotates 4/7 of a turn. Since 8/7 of a turn is the same as 1/7 of a turn, we can say there are 3 heptagons rotating, each twice as fast as the previous one! Greg Egan has made a movie of this in the Poincare dual picture where the Klein quartic is tiled by 56 triangles:”:
I like your use of color which allows for easier visualization.
Brandon Carter, “Micro-Anthropic Principle for Quantum theory”, effectively uses red, green, blue print within black text to highlight related concepts.
http://arxiv.org/abs/quant-ph/0503113
Post a Comment
<< Home