M Theory Lesson 284

Recall that there are three two-vertex ternary trees. Since binary trees (vertices of associahedra) are described by fully chorded (ie. triangulated) polygons, we now expect to cut up polygons into squares, since the four sides correspond to the $4$-valent vertex of a ternary tree. 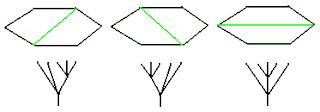Only polygons with an even number of sides appear. For the hexagon, the three ternary trees are described by three single chord diagrams. But these particular diagrams also have an interpretation in terms of binary trees! That is, they represent the three square faces of our favourite associahedron, which Loday matched to the crossings of a trefoil knot in three dimensional space. These binary trees each have five leaves, just like the ternary trees in the diagram above. The difference is that each ternary vertex has been resolved into two binary vertices using the rule: