M Theory Lesson 311
Under the correspondence between ribbon twists and roots of unity, as in  there is a matching of particle ribbon diagrams to matrices, giving in particular
there is a matching of particle ribbon diagrams to matrices, giving in particular  Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,
Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,  Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by
Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by 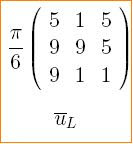 which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
 there is a matching of particle ribbon diagrams to matrices, giving in particular
there is a matching of particle ribbon diagrams to matrices, giving in particular  Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,
Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,  Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by
Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by  which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.







2 Comments:
OK Carl, so recall that the Fourier operator (F_3) has columns that are eigenvectors for a MUB Pauli (in 3d) ... and it's the Fouriers that give us neutrino mixing.
So we should take the eigenvectors of the phase matrices for the up quarks and the down quarks ... create matrices from the columns ... combine them ... compare to CKM ...
I did one by hand, and I seem to get suitably random looking numbers (19 \pm sqrt(57) etc) ... but this needs a bit more care ...
P.S. Neutrino TBM also uses F_2, but this is just the 2-circulant case, and there should be analogues for the quarks.
Post a Comment
<< Home