Arcadian Functor
occasional meanderings in physics' brave new world
Saturday, April 10, 2010
Not sure if this will work out, but future posts should appear at Arcadian Pseudofunctor.
Women at Work
Until the 1200s women in Europe often worked for a living, even for themselves, and played prominent roles in public life. It was the priests and noble women who learned to read, because noble men had to focus on fighting. The slow demise of women was undoubtedly heavily influenced by Christian thought, but as an institution the Church was not solely responsible for curbing their rights.
An early culprit was that fine new European institution, the University. Historically, many women had practised empirical medicine, but from 1271 the University of Paris insisted upon formal certification. By the early 1300s, women were being prosecuted for practicing medicine unlawfully. One example is Jacqueline Felicie de Alemania.
In Opera Muliebra, David Herlihy argues that women continued to be employed in many professions up until the population growth of the 1400s, after the great plague. In this century the power of the professional guilds was largely responsible for excluding women from apprenticeships.
The Church had tried to put women in their place for a millenium, without much success. The overriding factor in this story is that urban men wanted good work, once they had stopped fighting each other, and this was most easily achieved by excluding women, with excuses from Christian thought.
An early culprit was that fine new European institution, the University. Historically, many women had practised empirical medicine, but from 1271 the University of Paris insisted upon formal certification. By the early 1300s, women were being prosecuted for practicing medicine unlawfully. One example is Jacqueline Felicie de Alemania.
In Opera Muliebra, David Herlihy argues that women continued to be employed in many professions up until the population growth of the 1400s, after the great plague. In this century the power of the professional guilds was largely responsible for excluding women from apprenticeships.
The Church had tried to put women in their place for a millenium, without much success. The overriding factor in this story is that urban men wanted good work, once they had stopped fighting each other, and this was most easily achieved by excluding women, with excuses from Christian thought.
Thursday, April 08, 2010
Dwarf Mysteries
Universe Today reports on the discovery of a companion to the brown dwarf 2M J044144. 
Astronomers say it is the right size for a planet, but they believe the object formed in less than 1 million years — the approximate age of the brown dwarf — and much faster than the predicted time it takes to build planets according to conventional theories.Louise Riofrio predicted years ago that such planets would be found, because planets can form around tiny black holes. Thanks to Hubble and Gemini for these beautiful images.

Tuesday, April 06, 2010
M Theory Lesson 312
Let us now take two quark matrices and multiply them together. Using the phase matrices (in terms of $12$-th roots) on the MUB side of the twisted Fourier transform, for anti-up and anti-down quarks, we find that the product is  a positron in the dual braid space. This is a complementarity between quarks and leptons, taking full magic matrices to fun operators.
a positron in the dual braid space. This is a complementarity between quarks and leptons, taking full magic matrices to fun operators.
 a positron in the dual braid space. This is a complementarity between quarks and leptons, taking full magic matrices to fun operators.
a positron in the dual braid space. This is a complementarity between quarks and leptons, taking full magic matrices to fun operators.
Monday, April 05, 2010
Quote of the Week
Disgruntled, unemployed male postdoc:
Science has withstood the Catholic Church and its death threats. Science is not gonna go down to a bunch of feminists.
Sunday, April 04, 2010
M Theory Lesson 311
Under the correspondence between ribbon twists and roots of unity, as in  there is a matching of particle ribbon diagrams to matrices, giving in particular
there is a matching of particle ribbon diagrams to matrices, giving in particular  Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,
Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,  Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by
Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by 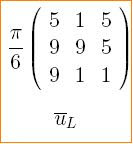 which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
 there is a matching of particle ribbon diagrams to matrices, giving in particular
there is a matching of particle ribbon diagrams to matrices, giving in particular  Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,
Observe how two copies of each $1$-circulant set arise from the choice of crossings in the braid diagram. Complex conjugacy is a flip of crossings. Given these matrices, a twisted Fourier transform of the form $F C_{a} F^{\dagger} = DC_{b}$, for $D$ a phased diagonal, takes MUB type operators $C_{a}$ to particle circulants $C_{b}$. For example,  Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by
Let us not forget the quarks! Quarks do not correspond to basis circulants, so under the inverse twisted transform they come from more general matrices. For example, the $C_a$ phases of an up quark are given by  which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
which is clearly not a MUB operator. Note, however, that this is a magic matrix, with all rows and columns summing to $- \pi / 6$.
Saturday, April 03, 2010
M Theory Lesson 310
Permutations may be represented by symmetric braids. A category theorist would usually draw a diagram like  indicating that the braid crossing goes neither over nor under, and that one can slide strands across each other. It would be nicer if we could draw a braid like
indicating that the braid crossing goes neither over nor under, and that one can slide strands across each other. It would be nicer if we could draw a braid like  because this obviously untangles to the identity braid. However, the two crossings here are different, like in the law $(\sigma) \circ (- \sigma) = 1$, which is to say that $\sigma$ is a bit like the complex $i$, satisfying $i + i^{-1} = 0$. How about elements of $S_3$? The permutation $(231)$ cubes to the identity, as in the diagram
because this obviously untangles to the identity braid. However, the two crossings here are different, like in the law $(\sigma) \circ (- \sigma) = 1$, which is to say that $\sigma$ is a bit like the complex $i$, satisfying $i + i^{-1} = 0$. How about elements of $S_3$? The permutation $(231)$ cubes to the identity, as in the diagram  where the crossings have been chosen so that no strand actually links with any other. Note that each $(231)$ section is a Bilson-Thompson braid. What fun! By assigning $n$-th roots of unity to each strand one obtains a fun operator, for $S_d$. The choice $n = d+1$ (see last time) gives a representation of $S_n$.
where the crossings have been chosen so that no strand actually links with any other. Note that each $(231)$ section is a Bilson-Thompson braid. What fun! By assigning $n$-th roots of unity to each strand one obtains a fun operator, for $S_d$. The choice $n = d+1$ (see last time) gives a representation of $S_n$.
 indicating that the braid crossing goes neither over nor under, and that one can slide strands across each other. It would be nicer if we could draw a braid like
indicating that the braid crossing goes neither over nor under, and that one can slide strands across each other. It would be nicer if we could draw a braid like  because this obviously untangles to the identity braid. However, the two crossings here are different, like in the law $(\sigma) \circ (- \sigma) = 1$, which is to say that $\sigma$ is a bit like the complex $i$, satisfying $i + i^{-1} = 0$. How about elements of $S_3$? The permutation $(231)$ cubes to the identity, as in the diagram
because this obviously untangles to the identity braid. However, the two crossings here are different, like in the law $(\sigma) \circ (- \sigma) = 1$, which is to say that $\sigma$ is a bit like the complex $i$, satisfying $i + i^{-1} = 0$. How about elements of $S_3$? The permutation $(231)$ cubes to the identity, as in the diagram  where the crossings have been chosen so that no strand actually links with any other. Note that each $(231)$ section is a Bilson-Thompson braid. What fun! By assigning $n$-th roots of unity to each strand one obtains a fun operator, for $S_d$. The choice $n = d+1$ (see last time) gives a representation of $S_n$.
where the crossings have been chosen so that no strand actually links with any other. Note that each $(231)$ section is a Bilson-Thompson braid. What fun! By assigning $n$-th roots of unity to each strand one obtains a fun operator, for $S_d$. The choice $n = d+1$ (see last time) gives a representation of $S_n$.
Friday, April 02, 2010
M Theory Lesson 309
Recall that much of the tribimaximal mixing literature discusses small finite groups, such as $S_3$ and $A_4$. For example, Ernest Ma considers a $2 \times 2$ representation of the six element group given by the matrices  where $\omega$ is the usual root of unity. This is an example of a fun set, with $d = 2$ and $n = 3$. In fact, it is the full such set under the condition that the non zero entries multiply to $1$. So special representations need no longer live in boring categories of vector spaces!
where $\omega$ is the usual root of unity. This is an example of a fun set, with $d = 2$ and $n = 3$. In fact, it is the full such set under the condition that the non zero entries multiply to $1$. So special representations need no longer live in boring categories of vector spaces!
 where $\omega$ is the usual root of unity. This is an example of a fun set, with $d = 2$ and $n = 3$. In fact, it is the full such set under the condition that the non zero entries multiply to $1$. So special representations need no longer live in boring categories of vector spaces!
where $\omega$ is the usual root of unity. This is an example of a fun set, with $d = 2$ and $n = 3$. In fact, it is the full such set under the condition that the non zero entries multiply to $1$. So special representations need no longer live in boring categories of vector spaces!
Meanwhile II
So I've found a suitable proof reader for my book, am busy hunting down literary agents, and am making progress with exciting, although naturally temporary, alternative career options. Now if, and it is a big if, any of these avenues should land me in the UK again, where should I spend some time? Hmm. I wonder what Cambridge is like ...





