M Theory Lesson 242
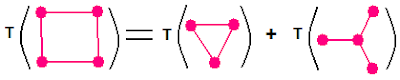 since any tree with $n$ edges has Tutte polynomial $x^{n}$. In fact, for any polygon we have $T_{n} = T_{n - 1} + \overline{T_{n-1}}$. What does this duality mean? Observe that a triangle plus a trivalent node can make a tetrahedron, so the square can be thought of as representing the four faces of a tetrahedron in three dimensions, which is the dimension of the MUB operators of $T_{4}$.
since any tree with $n$ edges has Tutte polynomial $x^{n}$. In fact, for any polygon we have $T_{n} = T_{n - 1} + \overline{T_{n-1}}$. What does this duality mean? Observe that a triangle plus a trivalent node can make a tetrahedron, so the square can be thought of as representing the four faces of a tetrahedron in three dimensions, which is the dimension of the MUB operators of $T_{4}$. It follows that a polygon with $n$ sides represents the $n$ faces of an $n$-simplex. The Tutte terms then match cells of the simplex: for $n = 4$, $x^{3}$ is a 3-cell, $x^{2}$ is a 2-cell and $x$ is a single edge. The oddball $y$ term comes from the loop on a single vertex.
Since the dual star graph puts three vertices in the region outside the trefoil knot on the plane, it marks three points in the plane, which we will call 0, 1 and $\infty$ as usual. This is like drawing a trefoil on an associahedron, the dual cell complex of which divides $\mathbb{R}^{3}$ into 9 regions, three of which are the square faces of the trefoil knot crossings. When the associahedron is drawn on the pair of pants, the central vertex of the trivalent node is marked with the number $\omega$. Thus the Tutte map $t \mapsto T(t)$ for $t = \omega$ (at $n = 4$) is a symmetry of the associahedron, which swaps sides of the pair of pants, or equivalently, acts via complex conjugation on the Belyi diagram for the j invariant.
In this paper the authors show that the Jones polynomial for any link can be obtained from a ribbon graph (dessins) diagram for planar link projections via a (three variable) generalisation of the Tutte polynomial, called the Bollobas-Riordan-Tutte polynomial.