At home again
Meanwhile, Carl threw a blog party to celebrate the mysterious growing interest in his amateur physics.
occasional meanderings in physics' brave new world

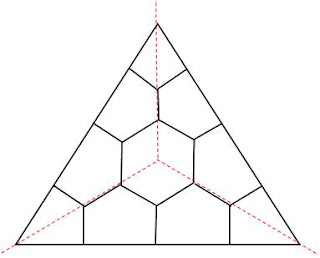 with 6 edges on the interior and 12 on the outside. Recall that the red lines mark individual 3x3 matrix corners. By staring at this picture we see a 3D chair corner with a little cube cut out of it. Using very regular such triangles to tile a plane, and then forgetting the triangular boundaries, we obtain a regular hexagonal tiling with hexagons the size of the interior hexagons, because each triangle vertex gives one sixth of a hexagon. There is then a second hexagonal tiling with hexagons made out of 6 big triangles. The big hexagons are 27 times the area of the little ones, since there are $4 \frac{1}{2}$ hexagons to a triangle.
with 6 edges on the interior and 12 on the outside. Recall that the red lines mark individual 3x3 matrix corners. By staring at this picture we see a 3D chair corner with a little cube cut out of it. Using very regular such triangles to tile a plane, and then forgetting the triangular boundaries, we obtain a regular hexagonal tiling with hexagons the size of the interior hexagons, because each triangle vertex gives one sixth of a hexagon. There is then a second hexagonal tiling with hexagons made out of 6 big triangles. The big hexagons are 27 times the area of the little ones, since there are $4 \frac{1}{2}$ hexagons to a triangle. where a diagonal that splits a hexagon in two corresponds to a square. This shows how pentagons may be paired, by taking dual diagonals, but squares are at best self dual. Labelled trees may be replaced by labelled polygons.
where a diagonal that splits a hexagon in two corresponds to a square. This shows how pentagons may be paired, by taking dual diagonals, but squares are at best self dual. Labelled trees may be replaced by labelled polygons. with two generating holes X and Y. So knots are expressed as words in X and Y. In Robert Ghrist's paper Branched two-manifolds supporting all links he shows that the template $\mathcal{V}_0$
with two generating holes X and Y. So knots are expressed as words in X and Y. In Robert Ghrist's paper Branched two-manifolds supporting all links he shows that the template $\mathcal{V}_0$  on more letters contains an isotopic copy of every (tame) knot and link. More specifically, for a parameter range $\beta \in [6.5,10.5]$ every link appears as a periodic solution to the equation
on more letters contains an isotopic copy of every (tame) knot and link. More specifically, for a parameter range $\beta \in [6.5,10.5]$ every link appears as a periodic solution to the equation  which is used to model an electric circuit. This is cool stuff. In M Theory we like ribbon diagrams which are twisted into loops like in the Lorenz template diagram. The universal template $\mathcal{V}_0$ can be embedded in an infinite sequence of more complicated templates, which in turn are embeddable in $\mathcal{V}_0$. Ghrist also considers flows arising from fibrations, such as the 1-punctured torus fibration for the figure 8 knot complement. This fibration flow is also an example of a universal flow.
which is used to model an electric circuit. This is cool stuff. In M Theory we like ribbon diagrams which are twisted into loops like in the Lorenz template diagram. The universal template $\mathcal{V}_0$ can be embedded in an infinite sequence of more complicated templates, which in turn are embeddable in $\mathcal{V}_0$. Ghrist also considers flows arising from fibrations, such as the 1-punctured torus fibration for the figure 8 knot complement. This fibration flow is also an example of a universal flow. As nosy snoopy noted, these crystal Calabi-Yau papers are really very interesting. I would like to know more about these random partitions. Okounkov has some notes here.
As nosy snoopy noted, these crystal Calabi-Yau papers are really very interesting. I would like to know more about these random partitions. Okounkov has some notes here.... the corpus of mathematics does resemble a biological entity which can only survive as a whole and would perish if separated into disjoint pieces.
 Actually, it's freezing down here, but the northern summer is conference time! Later this month the northern hemisphere sees both Loops 07 in Mexico and Strings 07 in Spain. Closer to home in early July, we have GRG18 in Sydney (conference venue in photo). No doubt many other interesting conferences are also coming up soon.
Actually, it's freezing down here, but the northern summer is conference time! Later this month the northern hemisphere sees both Loops 07 in Mexico and Strings 07 in Spain. Closer to home in early July, we have GRG18 in Sydney (conference venue in photo). No doubt many other interesting conferences are also coming up soon. This particular Hurwitz function is simply $\zeta_{H}(s) = (2^s - 1) \zeta (s)$, a simple multiple of the Riemann zeta function. According to Mathworld it has the interesting functional relation
This particular Hurwitz function is simply $\zeta_{H}(s) = (2^s - 1) \zeta (s)$, a simple multiple of the Riemann zeta function. According to Mathworld it has the interesting functional relation