Arcadian Functor
occasional meanderings in physics' brave new world
Wednesday, September 30, 2009
The next in a series of conferences that I intend to participate in is HEP in the LHC era. This is in Chile in January. It is a wonderful part of the world, which I highly recommend visiting.
Tuesday, September 29, 2009
One Wonders
Wasted paper, I guess. One does wonder about the other worlds that some people live in. From the Government Office for Science:
Rigour, respect and responsibility: A universal ethical code for scientists
Rigour, honesty and integrity
*Act with skill and care in all scientific work. Maintain up to date skills and assist their development in others.
*Take steps to prevent corrupt practices and professional misconduct. Declare conflicts of interest.
*Be alert to the ways in which research derives from and affects the work of other people, and respect the rights and reputations of others.
Responsible communication: listening and informing
*Seek to discuss the issues that science raises for society. Listen to the aspirations and concerns of others.
*Do not knowingly mislead, or allow others to be misled, about scientific matters. Present and review scientific evidence, theory or interpretation honestly and accurately.
Rigour, respect and responsibility: A universal ethical code for scientists
Rigour, honesty and integrity
*Act with skill and care in all scientific work. Maintain up to date skills and assist their development in others.
*Take steps to prevent corrupt practices and professional misconduct. Declare conflicts of interest.
*Be alert to the ways in which research derives from and affects the work of other people, and respect the rights and reputations of others.
Responsible communication: listening and informing
*Seek to discuss the issues that science raises for society. Listen to the aspirations and concerns of others.
*Do not knowingly mislead, or allow others to be misled, about scientific matters. Present and review scientific evidence, theory or interpretation honestly and accurately.
Monday, September 28, 2009
Publications
For many years people told me that, without a PhD, nobody would take me seriously. For the last few years people have been telling me that, without published papers, nobody would take me seriously. At 42, I think I get the idea. I cannot even apply for physics jobs without reference letters from professional physicists, even though many people I know apply for (and get) physics jobs without ever having studied physics.
But now it seems that Carl Brannen is publishing papers on quantum gravity left, right and centre! In respectable journals! Will people keep telling me not to waste my time with such amateurs? Will they keep saying I should focus on doing respectable science? What does that mean, anyway?
But now it seems that Carl Brannen is publishing papers on quantum gravity left, right and centre! In respectable journals! Will people keep telling me not to waste my time with such amateurs? Will they keep saying I should focus on doing respectable science? What does that mean, anyway?
Sunday, September 27, 2009
October
Organised and ready for the weeks ahead. A total of 5 tickets acquired ... from the bus station in Oxford to Mt Cook village in New Zealand.
Saturday, September 26, 2009
Mars Ice
An article in Science explains that new crater sites on Mars indicate more water on the planet than previously thought:
Thermal models of one site show that millimeters of sublimation occurred during this fading period, indicating clean ice rather than ice in soil pores.This follows confirmation of large amounts of lunar water.
Friday, September 25, 2009
M Theory Lesson 297
A Markov chain for a three state system has a $3 \times 3$ transition matrix, with entry $A_{ij}$ the probability that the system transitions from state $i$ to state $j$.
If the system is time symmetric, the matrix is both symmetric and magic, in that all rows and columns will sum to $1$. But for time asymmetric systems, it is only necessary that the columns sum to $1$. Matrix multiplication stands for one step in the Markov process. A typical long time convergence will result in a matrix of the form:
a a a
b b b
c c c
In fact, if all entries of $A^{k}$ (for some $k$) are strictly positive, then this always happens, and the limiting vector is called the steady state vector for the system.
If the system is time symmetric, the matrix is both symmetric and magic, in that all rows and columns will sum to $1$. But for time asymmetric systems, it is only necessary that the columns sum to $1$. Matrix multiplication stands for one step in the Markov process. A typical long time convergence will result in a matrix of the form:
a a a
b b b
c c c
In fact, if all entries of $A^{k}$ (for some $k$) are strictly positive, then this always happens, and the limiting vector is called the steady state vector for the system.
Tuesday, September 22, 2009
Seminar Thursday
It seems that there will be an interesting seminar on Thursday at the University of Warwick!
Sunday, September 20, 2009
Conference II
Hah! The security guards happily let me into St Annes, and the lovely conference organiser asked Joseph Silk whether I could be let in. He refused. Apparently the theatre is very full and there is simply no space.
Shall we test them? There are about 60 particiants. The lecture theatre seats 100 people. Now I am guessing that people will be keen on skipping some lectures tomorrow and the next day. Would any participants be willing to offer me their valuable seat for a lecture that they are not interested in attending?
Shall we test them? There are about 60 particiants. The lecture theatre seats 100 people. Now I am guessing that people will be keen on skipping some lectures tomorrow and the next day. Would any participants be willing to offer me their valuable seat for a lecture that they are not interested in attending?
Conference
I just found out about a cosmology conference around the corner from my office! Hah, let's see if I can gatecrash this YACWNW ...
Quote of the Month
Ben Barres gave a great seminar today, but his work is much better than his sister’s work.Statement by faculty member after the unpublicised female-male sex change of a transgendered academic.
Saturday, September 19, 2009
Tipping the Scales
I grow very weary of phrases along the lines of: the structure of quantum spacetime at the Planck scale.
Friday, September 18, 2009
Frontiers of Physics
Any physicists near Perth in November, who are looking for something to do, can meet Carl and me at the conference on Frontiers of Fundamental and Computational Physics at the University of Western Australia. We will both be speaking, and I am looking forward to the beach!
Thursday, September 17, 2009
Out on a Planck
 Today Planck reports its first results!
Today Planck reports its first results! The First Light Survey was completed on 27 August, yielding maps of a strip of the sky, one for each of Planck’s nine frequencies. Each map is a ring about 15 degrees wide, stretching across the full sky. Preliminary analysis indicates that the quality of the data is excellent.
M Theory Lesson 295
A while back we looked at ways of counting constrained paths that give, say, Motzkin or Schroeder numbers.
The Catalan number $C(n)$ counts the number of vertices on an associahedron polytope in dimension $n-3$, which is labelled by an $n$-gon. The generalised Catalan numbers $C(p,n)$ are given by
$C(p,n) = \frac{1}{n - 1} B(p (n - 2); (n - 2))$
for the binomial coefficient $B(n;k)$. The usual Catalan numbers are recovered when $p=2$. For example, $C(5) = 5$ gives the $5$ vertices of the pentagon in dimension $2$. The case $p=2$ is for binary trees. $C(p,n)$ is related to $p$-ary trees. For example, in lesson 284 we looked at the case $p=3$, which divides polygons into square pieces. The generalised Catalan number $C(p,n)$ is also used to count the number of paths on a lattice (from the origin) lying below the line of slope $p-1$.
The Catalan number $C(n)$ counts the number of vertices on an associahedron polytope in dimension $n-3$, which is labelled by an $n$-gon. The generalised Catalan numbers $C(p,n)$ are given by
$C(p,n) = \frac{1}{n - 1} B(p (n - 2); (n - 2))$
for the binomial coefficient $B(n;k)$. The usual Catalan numbers are recovered when $p=2$. For example, $C(5) = 5$ gives the $5$ vertices of the pentagon in dimension $2$. The case $p=2$ is for binary trees. $C(p,n)$ is related to $p$-ary trees. For example, in lesson 284 we looked at the case $p=3$, which divides polygons into square pieces. The generalised Catalan number $C(p,n)$ is also used to count the number of paths on a lattice (from the origin) lying below the line of slope $p-1$.
Wednesday, September 16, 2009
Tuesday, September 15, 2009
End/Start of Summer
The last weeks in Oxford are looking eventful, with the new term now approaching. Who knows? Perhaps I will make the opera in London before I leave. Meanwhile, plans are being made for the beautiful southern summer in the mountains.
Saturday, September 12, 2009
A Wedding
Today is Let's Embarrass Jamie Vicary Day! On this stunning summer's day, the young Jamie gets married to the lovely Laura! Congratulations to them both.
Friday, September 11, 2009
M Theory Lesson 294
Recall that the associahedra polytopes are labeled by chorded polygons. For example, the vertices and edges of the pentagon (the associahedron in the plane) are given as a five sided polygon with either one or two chords.  In category theory, the edges of the associahedron may be directed. This can be achieved by choosing a root edge on the index polygon, which is the same as selecting a root for the dual tree. A natural source (target) for the full polytope is then given by the fully left (right) branching tree. But for many purposes, where the cyclic symmetry is relevant, we need not select a root edge.
In category theory, the edges of the associahedron may be directed. This can be achieved by choosing a root edge on the index polygon, which is the same as selecting a root for the dual tree. A natural source (target) for the full polytope is then given by the fully left (right) branching tree. But for many purposes, where the cyclic symmetry is relevant, we need not select a root edge.
 In category theory, the edges of the associahedron may be directed. This can be achieved by choosing a root edge on the index polygon, which is the same as selecting a root for the dual tree. A natural source (target) for the full polytope is then given by the fully left (right) branching tree. But for many purposes, where the cyclic symmetry is relevant, we need not select a root edge.
In category theory, the edges of the associahedron may be directed. This can be achieved by choosing a root edge on the index polygon, which is the same as selecting a root for the dual tree. A natural source (target) for the full polytope is then given by the fully left (right) branching tree. But for many purposes, where the cyclic symmetry is relevant, we need not select a root edge.
Wednesday, September 09, 2009
Perpetual Summer
With the changing seasons will come a return to the south. I may have lined up a waitressing job for the busy southern summer. Meanwhile, check out this new academic jobs site: provide the usual data, and apply for hundreds of jobs at once!
Tuesday, September 08, 2009
Quote of the Summer
... so in philosophy, when we make use of false principles, we depart the farther from the knowledge of truth and wisdom exactly in proportion to the care withRene Descartes
which we cultivate them, and apply ourselves to the deduction of diverse consequences from them, thinking that we are philosophizing well, while we are only departing the farther from the truth; from which it must be inferred that they who have learned the least of all that has been hitherto distinguished by the name of philosophy are the most fitted for the apprehension of truth.
Monday, September 07, 2009
viXra Reading
Some interesting recent papers from the viXra preprint archive:
On Information Geometry, by Chris Goddard
Solar System Dynamics, by A. L. Kholodenko
Study of Supernovae Dimming, by T. B. Andrews
Keplerian Polyhedral Models, by Tony Smith
On Information Geometry, by Chris Goddard
Solar System Dynamics, by A. L. Kholodenko
Study of Supernovae Dimming, by T. B. Andrews
Keplerian Polyhedral Models, by Tony Smith
Mass Gap Revisited
In a theory with cosmologically varying masses, to some approximation there is no mass gap in the sense that a neutrino mass tends to zero in the early universe, at least from the point of view of a distant observer.
However, the standard model is only about local observations. And so as a matter of principle, given that we do not occupy the early universe, there must be a mass gap, given by the mass of the lightest neutrino, namely $0.00039$ eV.
In lecture 4B (you did watch it, right?) Arkani-Hamed discusses locality in terms of factorization for the coefficients of singularities that arise when internal lines in an old fashioned Feynman diagram go on-shell. This dictates how a proper four particle vertex with helicity labels should decompose into two three particle vertices. There are only two kinds of three particle vertex: (--+) and (-++).
It can be shown that factorization only allows two possible spin values, for a vertex with all legs having the same spin $s$. That is, either $s = 0$ or $s = 2$. Sound familiar? Spin $1$ Yang-Mills theory is OK if we mix spin values on the inputs. In that case, factorization says that the amplitudes must come from Lie group type structures. So the presence of Lie groups is derived from locality. They are not fundamental.
However, the standard model is only about local observations. And so as a matter of principle, given that we do not occupy the early universe, there must be a mass gap, given by the mass of the lightest neutrino, namely $0.00039$ eV.
In lecture 4B (you did watch it, right?) Arkani-Hamed discusses locality in terms of factorization for the coefficients of singularities that arise when internal lines in an old fashioned Feynman diagram go on-shell. This dictates how a proper four particle vertex with helicity labels should decompose into two three particle vertices. There are only two kinds of three particle vertex: (--+) and (-++).
It can be shown that factorization only allows two possible spin values, for a vertex with all legs having the same spin $s$. That is, either $s = 0$ or $s = 2$. Sound familiar? Spin $1$ Yang-Mills theory is OK if we mix spin values on the inputs. In that case, factorization says that the amplitudes must come from Lie group type structures. So the presence of Lie groups is derived from locality. They are not fundamental.
Sunday, September 06, 2009
Varying Mass
Recently we considered time varying mass in the Riofrio cosmology.
This is not a new idea. In the viXra article, Against the Tide: A Critical Review by Scientists of How Physics and Astronomy Get Done (188 pages), there is an article by Halton Arp which includes a discussion of the quasar NGC 7603:
This is not a new idea. In the viXra article, Against the Tide: A Critical Review by Scientists of How Physics and Astronomy Get Done (188 pages), there is an article by Halton Arp which includes a discussion of the quasar NGC 7603:
Number 92 in my Atlas of Peculiar galaxies has a large companion on the end of a luminous arm. In 1971, a spectrum revealed that this companion had a 8000 km/sec higher redshift than the central, active Seyfert galaxy. This amount of excess redshift cannot be accomodated in the conventional picture where redshifts mean velocities in an expanding universe. They could not be at such different distances and be physically interacting.In 2002, an astro-ph paper, by M. Lopez-Corredoira and Carlos M. Gutierrez, described two even higher redshift objects sitting exactly on the filament connecting the two galaxies of the NGC 7603 system.
When Fred Hoyle heard about this he came up from the Cal Tech campus to my Carnegie office and asked to see the original picture. In 1972 he gave the prestigious Russell Lecture at the Seattle meeting of the American Astronomical Society and outlined a theory whereby younger galaxies radiated intrinsically redshifted photons. His theory of growing particle masses was a more general solution to the conventional field equations but was physically a Machian (not Einsteinian theory). At the end of the lecture he said the NGC 7603 observation created a crisis in physics and we needed to cross over the bridge to a radically more general physics.
Saturday, September 05, 2009
Amused
An experienced traveller quickly gets used to the idiosyncracies of a new place. When a newly arrived Canadian researcher told me of her shock at being unable to open a bank account at a local bank which actually owed her money, I simply laughed (but then I did assure her that I knew it wasn't funny). When a few English colleagues failed to obtain cash from the ATMs in Waterloo, Canada, I merely shrugged my shoulders. When it took six months to obtain a health insurance number, I never gave it a thought.
But the train ticketing system is just plain hilarious. Many years ago, on my first visit to India, after several weeks of moving around by train I remember the great feeling of accomplishment when I finally understood how to find myself an appropriate seat. I have often been told that they inherited bureaucracy from the English, as indeed my country also did, but only now do I understand how true that is. Anyway, I booked and paid for a return trip to London online, and requested the tickets be sent to my home address (the alternative is to go to the station and stand in the line to use the only unbroken automatic ticket collection machine). The tickets arrived today. So how many ticket stubs am I issued for a simple return trip to London, which is only a few stops away? Eight. That's right, eight. Nine if you count for the extra one containing my address. That's because each trip has a minimum of two tickets: one ticket and one seat reservation. Then there is a ticket stub for the record of payment, a bit like a receipt but one also gets one of those. The remaining three tickets are indecipherable records of further details about both the booking and the payment.
But the tickets arrived promptly and the friendly postman handed them to me personally, bringing back distant memories from my childhood, when the same postman would come by our house every day.
But the train ticketing system is just plain hilarious. Many years ago, on my first visit to India, after several weeks of moving around by train I remember the great feeling of accomplishment when I finally understood how to find myself an appropriate seat. I have often been told that they inherited bureaucracy from the English, as indeed my country also did, but only now do I understand how true that is. Anyway, I booked and paid for a return trip to London online, and requested the tickets be sent to my home address (the alternative is to go to the station and stand in the line to use the only unbroken automatic ticket collection machine). The tickets arrived today. So how many ticket stubs am I issued for a simple return trip to London, which is only a few stops away? Eight. That's right, eight. Nine if you count for the extra one containing my address. That's because each trip has a minimum of two tickets: one ticket and one seat reservation. Then there is a ticket stub for the record of payment, a bit like a receipt but one also gets one of those. The remaining three tickets are indecipherable records of further details about both the booking and the payment.
But the tickets arrived promptly and the friendly postman handed them to me personally, bringing back distant memories from my childhood, when the same postman would come by our house every day.
M Theory Lesson 293
Last time we considered chord flips on a square. Recall that a chorded square labels a point at the source or target of an associator edge.
A basic three leaf tree is what labels the associator edge. In other words, an associator edge is like two four point diagrams connected by a single three point diagram. This is backwards (or rather, Poincare dual) to the situation of interest in twistor QFT, which is where a four point vertex may factorize into pairs of three point vertices.
As it happens, there is such a thing as a dual square, where points become edges and edges points. In this context, roughly speaking, the square would be called a Hodges diagram. The vertices on a Hodges diagram stand for twistor variables in a massless field theory. Poincare duality is a simple enough idea, so massless particle physics really does see associahedra.
That's category theory, folks. You can keep saying that category theory has nothing to do with physics. But Nature does not agree with you.
A basic three leaf tree is what labels the associator edge. In other words, an associator edge is like two four point diagrams connected by a single three point diagram. This is backwards (or rather, Poincare dual) to the situation of interest in twistor QFT, which is where a four point vertex may factorize into pairs of three point vertices.
As it happens, there is such a thing as a dual square, where points become edges and edges points. In this context, roughly speaking, the square would be called a Hodges diagram. The vertices on a Hodges diagram stand for twistor variables in a massless field theory. Poincare duality is a simple enough idea, so massless particle physics really does see associahedra.
That's category theory, folks. You can keep saying that category theory has nothing to do with physics. But Nature does not agree with you.
Wednesday, September 02, 2009
New Worlds
The image below is taken from a paper by Ingrosso et al on the hunt for extrasolar planets in Andromeda. Yeah, no kidding. Here is the planet in the catalog, with a mass of $6.34 M_{J}$. 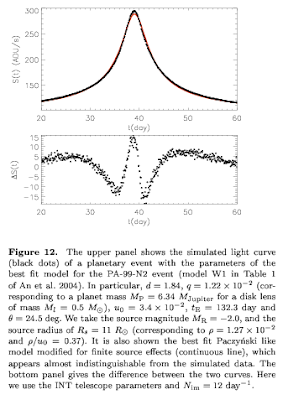

T Duality
Now that String Theory has officially won the String Wars* (by changing its thinking radically enough to finally look like it is on the right track) it is worth making a simple point about T duality.
In modern physics, almost everything is measured in terms of energy. Distance is an inverse energy, temperature is an energy, and so on. For a basic black hole, the mass of a black hole goes like the inverse of a Hawking temperature. In other words, mass is somehow like an inverse energy, which is the distance scale of the black hole radius.
But mass is just an energy. So even without considering any kind of string theory at all, we should expect T duality to play an important role in gravity.
In a non local theory, however, it does no good to talk about a priori distance scales. At the fundamental level, black hole properties arise from considerations of, say, their information content. It is expected that a classical spacetime, with its notion of horizon scale, should only arise as a thermodynamic collection of such quantum states. So where is the T duality? It can only be in the mass quantum numbers. Distances are derived from the masses, but they are not inherently properties of the quantum states. This suggests that a rigorous T duality for Yang-Mills theory is closely related to the issue of a mass gap, because the limit of the Planck scale is replaced by a minimal, or dually maximal, mass.
*AF will still occasionally refer to string theorists as idiots, and the correct theory as M theory.
In modern physics, almost everything is measured in terms of energy. Distance is an inverse energy, temperature is an energy, and so on. For a basic black hole, the mass of a black hole goes like the inverse of a Hawking temperature. In other words, mass is somehow like an inverse energy, which is the distance scale of the black hole radius.
But mass is just an energy. So even without considering any kind of string theory at all, we should expect T duality to play an important role in gravity.
In a non local theory, however, it does no good to talk about a priori distance scales. At the fundamental level, black hole properties arise from considerations of, say, their information content. It is expected that a classical spacetime, with its notion of horizon scale, should only arise as a thermodynamic collection of such quantum states. So where is the T duality? It can only be in the mass quantum numbers. Distances are derived from the masses, but they are not inherently properties of the quantum states. This suggests that a rigorous T duality for Yang-Mills theory is closely related to the issue of a mass gap, because the limit of the Planck scale is replaced by a minimal, or dually maximal, mass.
*AF will still occasionally refer to string theorists as idiots, and the correct theory as M theory.








